Pengertian Limit Trigonometri
Limit trigonometri adalah nilai terdekat suatu sudut pada fungsi trigonometri. Perhitungan limit fungsi trigonometri bisa langsung disubtitusikan seperti limit fungsi aljabar tetapi ada fungsi trigonometri yang harus diubah dulu ke identitas trigonometri untuk limit tak tentu yaitu limit yang apabila kita langsung subtitusikan nilainya bernilai 0, bisa juga untuk limit tak tentu tidak harus menggunakan identitas tetapi menggunakan teorema limit trigonometri atau ada juga yang menggunakan identitas dan teorema. Jadi apabila suatu fungsi limit trigonometri di subtitusikan nilai yang mendekatinya menghasilkan dan maka kita harus menyelesaikan dengan cara lain.
Untuk menentukan nilai limit suatu fungsi trigonometri terdapat beberapa cara yang bisa dipakai :
- Metode Numerik
- Subtitusi
- Pemfaktoran
- Kali Sekawan
- Menggunakan Turunan
Penulisan nya adalah sebagai berikut :
Cara membaca dari limit di atas yaitu limit fungsi f(x) untuk x mendekati c.
Macam- Macam Trigonometri dan Identitasnya
Macam-macam trigonometri
Berikut ini adalah nama-nama trigonometri yang kita kenal :
- Sinus (sin)
- Tangen (tan)
- Cosinus (cos)
- Cotongen (cot)
- Secan (sec)
- Cosecan (Csc)
Rumus kebalikan
Identitas Trigonometri
Rumus Jumlah dan Selisih
Rumus Perkalian
Rumus sudut rangkap
Teorema limit trigonometri
Ada beberapa teorema yang dapat digunakan untuk menyelesaikan persoalan limit trigonometri yaitu :
Teorema A
Teorema di atas hanya berlaku saat (x -> 0) .
Teorema B
Terdapat beberapa teorema yang berlaku. Untuk setiap bilangan real c di dalam daerah asal fungsi yaitu :
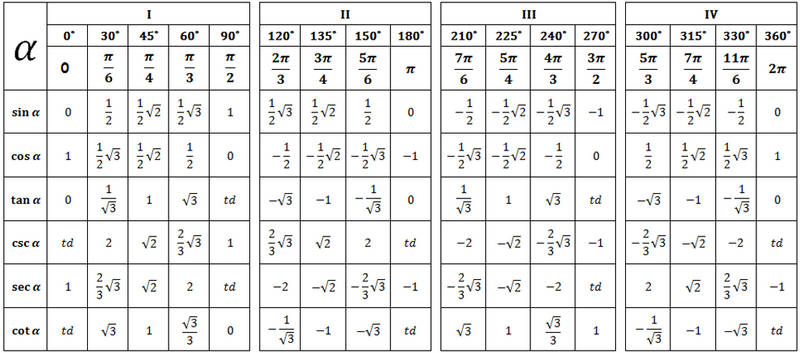
Biasanya dalam soal limit fungsi trigonometri nilai terdekat dari limit fungsinya yaitu berupa sudut sudut istimewa yaitu sudut yang memiliki nilai sederhana. Untuk itu kita perlu mengetahui nilai-nilai sudut istimewa yang disajikan table di bawah ini :
Agar lebih jelas dibawah ini terdapat beberapa contoh soal limit fungsi trigonometri
Contoh soal :
- Selesaikan limit trigonometri berikut :
Jawab ;
Melihat bentuk limit pada soal di atas kita dapat langsung mensubtitusikan nilai x.
- Selesaikan limit trigonometri berikut :
Jawab :
Melihat bentuk limit di atas makan kita dapat mengarahkan limit ke bentuk teorema A
Tetapi dalam soal fungsi sinus adalah 3x bukan x sebagaimana syarat dari teorema A. Maka kita dapat mengalikan fungsi dengan 1 agar nilainya tidak berubah
Dikali dengan 3/3 hal ini tidak merubah fungsi karena sama dengan di kali 1. Kemudian kita dapat memisalkan agar fungsi berbentuk seperti teorema A yaitu dengan memisalkan 3x.
Misal y=3x maka y –> jika dan. hanya jika x–>0 sehingga :
- Selesaikan limit trigonometri berikut :
Nilai
Jawab :
kita tidak dapat langsung mensubtitusikan nilai x ke fungsi dikarenakan haslnya akan 0 ini adalah contoh soal limit tak tentu. kita dapat memfaktorkan fungsi penyebut agar kita mendapat (x-2) sehingga berlaku teorema A
- Selesaikan limit trigonometri berikut : Nilai = …
Jawab :
jika kita subtitusikan maka nilainya 0 sehingga terlebih dahulu kita harus mengarahkan menjadi bentuk yang apabila kita subtitusikan nilainya ≠0
kita ubah fungsi menggunakan identitas sudut rangkap sehingga
1-cos4x=2sin 22x
- Selesaikan limit trigonometri dibawah ini
Jawab :
Karena apabila langsung di subtitusikan menghasilkan 0 maka kita perlu menyelesaikan soal di atas dengan mengubah ke bentuk identitas
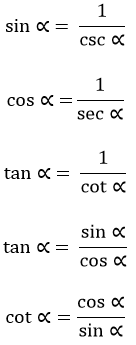

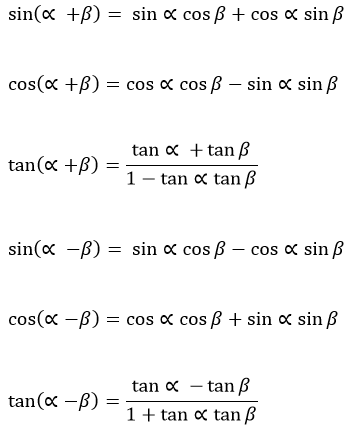
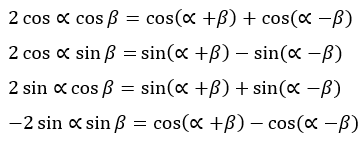
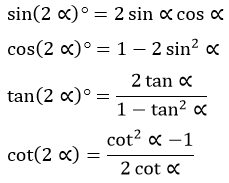
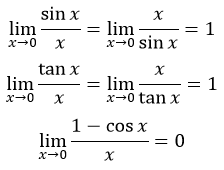
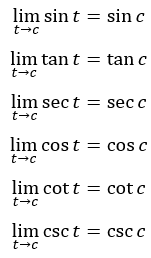
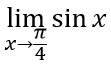

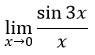

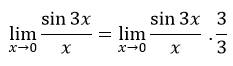
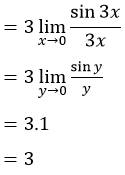

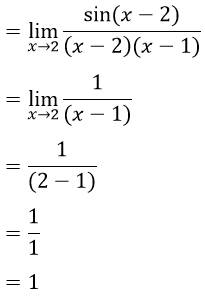

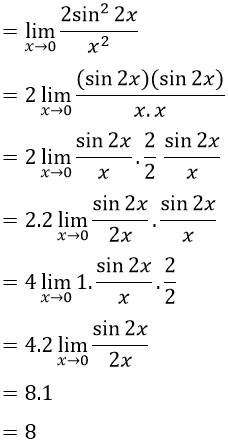
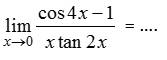
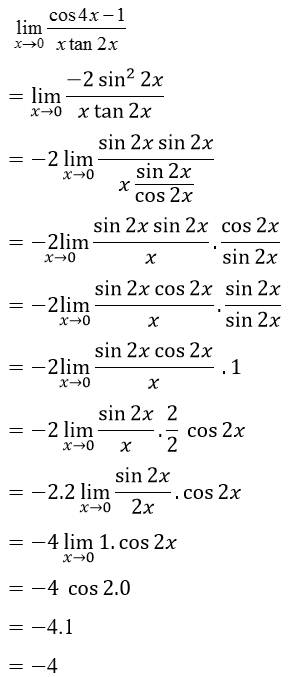
Komentar
Posting Komentar